A coordination compound is a complex compound which contains a metal bonded to ligands. A LIGAND can be an atom, an ion or a molecule that donates electrons to the metal.
Werner postulated the following theory:
- The central metal atom in a coordination compound exhibits two types of valences (linkages) – primary and secondary.
- Primary valences are generally ionisable and are satisfied by negative ions.
- The secondary valences are non-ionisable. These are generally satisfied by negative ions or neutral molecules. The secondary valence is fixed for a metal and is equal to the coordination number.
- The ions bounded by the secondary linkages to the metal exhibit characteristic spatial arrangements corresponding to different coordination numbers.
Such spatial arrangements are now known as coordination polyhedra. The species within the square brackets are called coordination entities or complexes and the ions outside the square brackets are known as counter ions.
Limitations of Werner’s Theory:
- It failed to explain why all elements don’t form coordination compounds.
- It failed to explain the directional properties of bonds in coordination compounds.
- It does not explain the colour, and the magnetic and optical properties shown by coordination compounds.
Structures of Metal Complexes:
The coordination numbers of metal ions in metal complexes can range from 2 to at least 9. In general, the differences in energy between different arrangements of ligands are greatest for complexes with low coordination numbers and decrease as the coordination number increases. Usually only one or two structures are possible for complexes with low coordination numbers, whereas several different energetically equivalent structures are possible for complexes with high coordination numbers (n > 6). The following presents the most commonly encountered structures for coordination numbers 2–9. Many of these structures should be familiar to you from our discussion of the valence-shell electron-pair repulsion (VSEPR) model because they correspond to the lowest-energy arrangements of n electron pairs around a central atom.
Compounds with low coordination numbers exhibit the greatest differences in energy between different arrangements of ligands.
Coordination Number 2
Although it is rare for most metals, this coordination number is surprisingly common for d10 metal ions, especially Cu+, Ag+, Au+, and Hg2+. An example is the [Au(CN)2]− ion, which is used to extract gold from its ores. As expected based on VSEPR considerations, these complexes have the linear L–M–L structure shown here.

Coordination Number 3
Although it is also rare, this coordination number is encountered with d10 metal ions such as Cu+ and Hg2+. Among the few known examples is the HgI3− ion. Three-coordinate complexes almost always have the trigonal planar structure expected from the VSEPR model.

Coordination Number 4
Two common structures are observed for four-coordinate metal complexes: tetrahedral and square planar. The tetrahedral structure is observed for all four-coordinate complexes of nontransition metals, such as [BeF4]2−, and d10 ions, such as [ZnCl4]2−. It is also found for four-coordinate complexes of the first-row transition metals, especially those with halide ligands (e.g., [FeCl4]− and [FeCl4]2−). In contrast, square planar structures are routinely observed for four-coordinate complexes of second- and third-row transition metals with d8electron configurations, such as Rh+ and Pd2+, and they are also encountered in some complexes of Ni2+ and Cu2+.

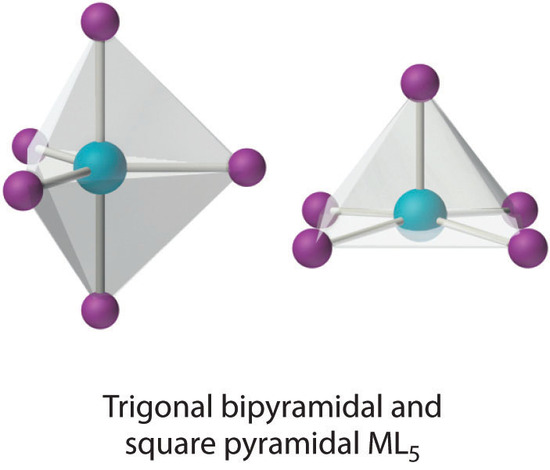
Coordination Number 5
This coordination number is less common than 4 and 6, but it is still found frequently in two different structures: trigonal bipyramidal and square pyramidal. Because the energies of these structures are usually rather similar for most ligands, many five-coordinate complexes have distorted structures that lie somewhere between the two extremes.
Coordination Number 6
This coordination number is by far the most common. The six ligands are almost always at the vertices of an octahedron or a distorted octahedron. The only other six-coordinate structure is the trigonal prism, which is very uncommon in simple metal complexes.

Coordination Number 7
This relatively uncommon coordination number is generally encountered for only large metals (such as the second- and third-row transition metals, lanthanides, and actinides). At least three different structures are known, two of which are derived from an octahedron or a trigonal prism by adding a ligand to one face of the polyhedron to give a “capped” octahedron or trigonal prism. By far the most common, however, is the pentagonal bipyramid.

Coordination Number 8
This coordination number is relatively common for larger metal ions. The simplest structure is the cube, which is rare because it does not minimize interligand repulsive interactions. Common structures are the square antiprism and the dodecahedron, both of which can be generated from the cube.

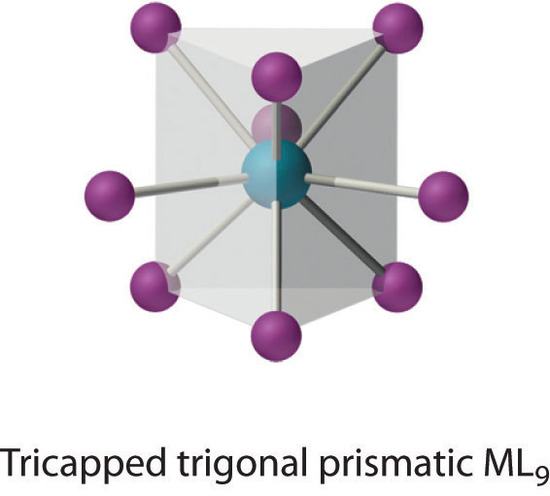
Coordination Number 9
This coordination number is found in larger metal ions, and the most common structure is the tricapped trigonal prism, as in [Nd(H2O)9]3+.