Context Free Languages

A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where

  • N is a set of non-terminal symbols.
  • T is a set of terminals where N ∩ T = NULL.
  • P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
  • S is the start symbol.

In formal language theory, a context-free grammar (CFG) is a certain type of formal grammar: a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the rule

 A\ \to \ \alpha

replaces  A with  \alpha . There can be multiple replacement rules for any given value. For example,

 A\ \to \ \alpha

 {\displaystyle A\ \to \ \beta }

means that  A can be replaced with either  \alpha  or   \beta .

In context-free grammars, all rules are one-to-one, one-to-many, or one-to-none. These rules can be applied regardless of context. The left-hand side of the production rule is also always a non-terminal symbol. This means that the symbol does not appear in the resulting formal language. So in our case, our language contains the letters  \alpha  and  \beta  but not  A. 

Rules can also be applied in reverse to check if a string is grammatically correct according to the grammar.

Here is an example context-free grammar that describes all two-letter strings containing the letters \alpha  and  \beta .

 {\displaystyle S\ \to \ AA}

 A\ \to \ \alpha

 {\displaystyle A\ \to \ \beta }

If we start with the non-terminal symbol  S then we can use the rule  {\displaystyle S\ \to \ AA} to turn  S into  AA. We can then apply one of the two later rules. For example, if we apply  {\displaystyle A\ \to \ \beta } to the first  A we get  {\displaystyle \beta A}. If we then apply  A\ \to \ \alpha  to the second  A we get  {\displaystyle \beta \alpha }. Since both  \alpha  and  \beta  are terminal symbols, and in context-free grammars terminal symbols never appear on the left hand side of a production rule, there are no more rules that can be applied. This same process can be used, applying the second two rules in different orders in order to get all possible strings within our simple context-free grammar.

Parse tree

A parse tree or parsing tree  or derivation tree or concrete syntax tree is an ordered, rooted tree that represents the syntactic structure of a string according to some context-free grammar. The term parse tree itself is used primarily in computational linguistics; in theoretical syntax, the term syntax tree is more common.

Parse trees concretely  reflect the syntax of the input language, making them distinct from the abstract syntax trees used in computer programming. Unlike Reed-Kellogg sentence diagrams used for teaching grammar, parse trees do not use distinct symbol shapes for different types of constituents.

Parse trees are usually constructed based on either the constituency relation of constituency grammars (phrase structure grammars) or the dependency relation of dependency grammars. Parse trees may be generated for sentences in natural languages (see natural language processing), as well as during processing of computer languages, such as programming languages.

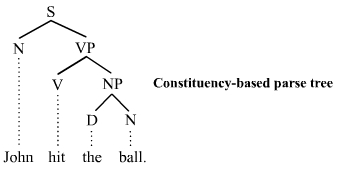
The constituency-based parse trees of constituency grammars (= phrase structure grammars) distinguish between terminal and non-terminal nodes. The interior nodes are labeled by non-terminal categories of the grammar, while the leaf nodes are labeled by terminal categories. The image below represents a constituency-based parse tree; it shows the syntactic structure of the English sentence John hit the ball:

Parse tree PSG

The parse tree is the entire structure, starting from S and ending in each of the leaf nodes (John, hit, the, ball). The following abbreviations are used in the tree:

  • S for sentence, the top-level structure in this example
  • NP for noun phrase. The first (leftmost) NP, a single noun “John”, serves as the subject of the sentence. The second one is the object of the sentence.
  • VP for verb phrase, which serves as the predicate
  • V for verb. In this case, it’s a transitive verb hit.
  • D for determiner, in this instance the definite article “the”
  • N for noun

Each node in the tree is either a root node, a branch node, or a leaf node.  A root node is a node that doesn’t have any branches on top of it. Within a sentence, there is only ever one root node. A branch node is a mother node that connects to two or more daughter nodes. A leaf node, however, is a terminal node that does not dominate other nodes in the tree. S is the root node, NP and VP are branch nodes, and John (N), hit (V), the (D), and ball (N) are all leaf nodes. The leaves are the lexical tokens of the sentence. A mother node is one that has at least one other node linked by a branch under it. In the example, S is a parent of both N and VP. A daughter node is one that has at least one node directly above it to which it is linked by a branch of a tree. From the example, hit is a daughter node of V. The terms parent and child are also sometimes used for this relationship.

 

PUSH DOWN AUTOMATION:

A pushdown automaton is a way to implement a context-free grammar in a similar way we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

Basically a pushdown automaton is −

“Finite state machine” + “a stack”

A pushdown automaton has three components −

  • an input tape,
  • a control unit, and
  • a stack with infinite size.

The stack head scans the top symbol of the stack.

A stack does two operations −

  • Push − a new symbol is added at the top.
  • Pop − the top symbol is read and removed.

We use standard formal language notation:  \Gamma ^{*} denotes the set of strings over alphabet  \Gamma  and  \varepsilon  denotes the empty string.

A PDA is formally defined as a 7-tuple:

 M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ Z,\ F) where

  •  \,Q is a finite set of states
  •  \,\Sigma  is a finite set which is called the input alphabet
  •  \,\Gamma  is a finite set which is called the stack alphabet
  •  \,\delta  is a finite subset of  Q\times (\Sigma \cup \{\varepsilon \})\times \Gamma \times Q\times \Gamma ^{*}, the transition relation.
  •  \,q_{0}\in \,Q is the start state
  •  \ Z\in \,\Gamma  is the initial stack symbol
  •  F\subseteq Q is the set of accepting states

An element  (p,a,A,q,\alpha )\in \delta  is a transition of  M. It has the intended meaning that  M, in state p\in Q, on the input  a\in \Sigma \cup \{\varepsilon \} and with  A\in \Gamma  as topmost stack symbol, may read  a, change the state to  q, pop  A, replacing it by pushing \alpha \in \Gamma ^{*}. The  (\Sigma \cup \{\varepsilon \}) component of the transition relation is used to formalize that the PDA can either read a letter from the input, or proceed leaving the input untouched.