Coulomb’s law

Coulomb’s law states that the electric force F between two charges is directly proportional to the multiplication of quantities of these charges and inversely proportional to the square of the distance between their centers.

F=k_{e}{\frac {q_{1}q_{2}}{r^{2}}}

where k_e is Coulomb’s constant (k_e = 8.99×10⁹ N m² C⁻²), q₁ and q₂ are the signed magnitudes of the charges, and the scalar r is the distance between the charges. The force of interaction between the charges is attractive if the charges have opposite signs

Electric field intensity

Force of the generated electric charges

Electric field intensity is a vector quantity, and therefore has a numerical value and direction. The electric field has a dimension that depends on the method of its calculation

Gauss’s Law

The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.

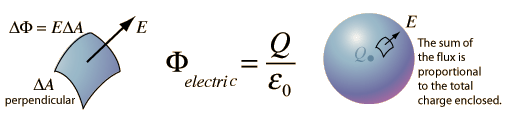The electric flux through an area is defined as the electric field multiplied by the area of the surface projected in a plane perpendicular to the field. Gauss’s Law is a general law applying to any closed surface. It is an important tool since it permits the assessment of the amount of enclosed charge by mapping the field on a surface outside the charge distribution. For geometries of sufficient symmetry, it simplifies the calculation of the electric field.

Another way of visualizing this is to consider a probe of area A which can measure the electric field perpendicular to that area. If it picks any closed surface and steps over that surface, measuring the perpendicular field times its area, it will obtain a measure of the net electric charge within the surface, no matter how that internal charge is configured.

summary

Name	Integral equations	Differential equations	Meaning
Gauss’s law	$\oiint$ ${\scriptstyle \partial \Omega }$ $\mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {1}{\varepsilon _{0}}}\iiint _{\Omega }\rho \,\mathrm {d} V$	$\nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}$	The electric flux leaving a volume is proportional to the charge inside.
Gauss’s law for magnetism	$\oiint$ ${\scriptstyle \partial \Omega }$ $\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0$	$\nabla \cdot \mathbf {B} =0$	There are no magnetic monopoles; the total magnetic flux through a closed surface is zero.
Maxwell–Faraday equation (Faraday’s law of induction)	$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S}$	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	The voltage induced in a closed loop is proportional to the rate of change of the magnetic flux that the loop encloses.
Ampère’s circuital law (with Maxwell’s addition)	$\oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} +\mu _{0}\varepsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {S}$	$\nabla \times \mathbf {B} =\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)$	The magnetic field induced around a closed loop is proportional to the electric current plus displacement current (rate of change of electric field) that the loop encloses.

conduction and displacement curent

conduction current: current in conductors due to flow of electron under applied electric potential”. This is usually the case where the surface charge density is small.
“displacement current: current b/w two plates of capacitors, due to electric field”. This is true for the space between two capacitor plates if the flux tubes connecting the source charges on the plates (displacement field) is varying in time. Of course, the displacement current is non-zero under all time varying displacement fields.