Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slope of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.
The idea is that while the curve is initially unknown, its starting point, which we denote by 

Take a small step along that tangent line up to a point 




Choose a value 


The value of 





While the Euler method integrates a first-order ODE, any ODE of order N can be represented as a first-order ODE: to treat the equation
-
,
we introduce auxiliary variables 
This is a first-order system in the variable 
Example
Given the initial value problem
we would like to use the Euler method to approximate 
Using step size equal to 1 (h = 1)
The Euler method is
so first we must compute 


By doing the above step, we have found the slope of the line that is tangent to the solution curve at the point 



The next step is to multiply the above value by the step size 
Since the step size is the change in 


The above steps should be repeated to find 


Due to the repetitive nature of this algorithm, it can be helpful to organize computations in a chart form, as seen below, to avoid making errors.
-
0 1 0 1 1 1 2 1 2 1 2 1 2 4 2 4 2 4 1 4 8 3 8 3 8 1 8 16
The conclusion of this computation is that 


Using other step sizes
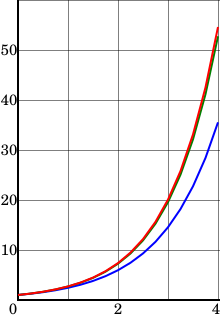
As suggested in the introduction, the Euler method is more accurate if the step size 
-
step size result of Euler’s method error 1 16 38.598 0.25 35.53 19.07 0.1 45.26 9.34 0.05 49.56 5.04 0.025 51.98 2.62 0.0125 53.26 1.34
The error recorded in the last column of the table is the difference between the exact solution at 
Other methods, such as the mid point method also illustrated in the figures, behave more favourably : the error of the midpoint method is roughly proportional to the square of the step size. For this reason, the Euler method is said to be a first-order method, while the midpoint method is second order.
We can extrapolate from the above table that the step size needed to get an answer that is correct to three decimal places is approximately 0.00001, meaning that we need 400,000 steps. This large number of steps entails a high computational cost. For this reason, people usually employ alternative, higher-order methods such as runge kutta method or linear multi step methods , especially if a high accuracy is desired
Derivation
The Euler method can be derived in a number of ways. Firstly, there is the geometrical description mentioned above.
Another possibility is to consider the taylor expansion of the function 

The differential equation states that 
A closely related derivation is to substitute the forward finite differences formula for the derivative,
in the differential equation 
Finally, one can integrate the differential equation from 

Now approximate the integral by the left-hand rectangle method (with only one rectangle):